BINARY
SEARCH:
Let aᵢ,
1≤ i ≤n, be a list of Elements that
are stored in non-decreasing order. Consider the problem of determining whether
a given element x is present in the list. If x is present, we are determine a
value j such that aj = x. If x is not in the list, then j is set
to be zero. Let P= (n, ai, …., al) denote
an arbitrary instance of this search problem (n is the number of elements in
the list, ai, …., al is the
list of elements, and x is the element for search for).
Divide-and-conquer
can be used to solve this problem. Let Small(P) be true if n = 1. In this case
S(P) will take the value i if x = ai
; Otherwise it will take the value 0.. Then g(1) = Θ(1). If P has more
than one element, it can be divided into a new sub-problem as follows. Pick an
index q in the range [i, l ] and compare x with aq. There are three
possibilities:
1.
x = aq : In this case the problem P
is immediately solved.
2.
x < aq : In this case x has to be
searched for only the sub-list ai,ai-1,….,aq-1,x).
3.
x > aq : In this case sublist to
be searched is aq+1,…..,al . P produces to ( l -q,aq+1,….,al,x).
In this example,
any given problem P gets divided into one new sub-problem. This division takes only
Θ(1)
time. After a comparison with aq , the instance remaining to the
solved (if any) can be solved by using this divide-and-conquer scheme again. If
q is always chosen such that aq is the middle element (i.e. q =
(n+1)/2), then the resulting search algorithm known as Binary Search. Note that
the answer of the new sub-problem is also the answer of original problem P;
There is no need for any combining.
Algorithm 1
describes this Binary Search method, where BinSearch has four input a[ ], i, l,
and x. It is initially involved as BinSearch( a, 1, n, x).
·
Algorithm 1: Recursive Binary Search
BinSearch(a[], i, l, x)
// Give an array a[i:l] of elements in
non-decreasing order,
// 1≤i≤l, determine whether x is present, and
if so, return j
// such that x = a[j]; else return 0.
{
if(l=i)
then // if Small(P)
{
if(x=a[i])
then return i;
else
return 0;
}
else
{
//Reduce
P into smaller Sub-Problem.
mid
= (i+l)/2;
if(x=a[mid])
then return mid;
else
return BinSearch(a,mid+1,l,x);
}
}
A
non-recursive version of BinSearch is given in Algorithm 2. BinSearch has three
inputs a, n, & x. The while loop continues processing as long as there more
elements left to check. At the conclusion of procedure 0 is return if x is not
present, or j is returned, such that a[j]=x.
Is BinSearch an algorithm? We must be
sure that all of the operations such as comparisons between x and a[mid] are
well defined. The relational operator carry out the comparisons among elements
of a correctly if these operators are appropriately defined.
Does BinSearch Terminate? We observe
that low & high are integer variable such that each time through the loop
either x is found or low is increased
by at least one or high is decreased
by at least one. Thus we have to sequences of integers approaching each other
and eventually low become greater
than high and cause termination in a
finite number of steps if x is not present.
·
Algorithm 2: Non-Recursive Binary Search
BinSearch(a,
n, x)
//
Give an array a[1:n] of elements in non-decreasing order, n≥0,
//
determine whether x is present, and if so, return j such that
//
x=a[j]; else return 0.
{
low:=1; high:=n;
while(low ≤ high)
{
mid:=(low+high)/2;
else if (x>a[mid]) then low:=mid+1;
else return mid;
}
return
0;
}
Example:
Let us
consider 14 entries:
-15,-6,0,7,9,23,54,82,101,112,125,131,142,151
Place them
in a[1:14] and simulate the steps that bin search goes through as it searches
for different values of x. Only the variables low, high and mid need to be
traced as we simulate the algorithm. We try the following values for x:
151,-14,9 for two successful searches and one unsuccessful search. The traces
of these three inputs shows below:
X = 151 low high mid
1 14 7
8 14 11
12 14 13
14 14 14
Found
X = -14 low high mid
1 14 7
1 6 3
1 2 1
2 2 2
2 1 Not Found
X = 9 low high mid
1 14 7
1 6 3
4 6 5
Found
To
test all successful searches, x must take on the n values for a. To test all unsuccessful
searches, x must take on the n+1 values for a. Thus complexity of BinSearch is
2n+1 for each n.
Now
Let analyze the execution profile of BinSearch. The two relevant characteristics
of this profile are the frequency count and space required of the n elements of
the array plus the variables low, high, mid and x, or n+4 locations. As for the
time, there are three possibilities to consider: the best, average and worst
cases.
Suppose
we begin determining the time for BinSearch on the previous data set. We
observe that the only operations in the algorithm are comparisons and some
arithmetic and data movements. We concentrate on comparisons between x and the
elements in a[ ], recognizing that the frequency count of all other operations
is of the same order as that for these comparisons. We assume that only one
comparisons needed to determine which of the three possibilities of the if
statement holds. The number of element comparison needed to find each of the 14
elements is
a:
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
[10]
|
[11]
|
[12]
|
[13]
|
[14]
|
Elements:
|
-15
|
-6
|
0
|
7
|
9
|
23
|
54
|
82
|
101
|
112
|
125
|
131
|
142
|
151
|
Comparisons:
|
3
|
4
|
2
|
4
|
3
|
4
|
1
|
4
|
3
|
4
|
2
|
4
|
3
|
4
|
No
elements require more than 4 comparisons to be found. The average is obtained
by summing the comparisons need to find all 14 items and dividing by 14. These yields
45/14, or approximately 3.21, comparisons per successful search on the average.
There are 15 possible ways that an unsuccessful search may terminate depending
on the value of x. If x
The
analysis just done applies to any stored sequence containing 14 elements. But
the result we would prefer is a formula for n elements. A good way to derive
such a formula plus a better way to understand the algorithm is to consider the
sequence of values for mid that are produced by BinSearch for all possible
values for x. These values are nicely described using a binary decision tree in
which the value in each node is the value of mid. For example , if n=14, then
below figure contain a binary decision tree that traces the way in which these
values are produced by BinSearch.
The first comparison is x with a[7]. If
xa[7], then
the next comparison is a[11]. Each path through the tree represents a sequence
of comparison in the binary search method. If x is present, then the algorithm
will end at one of the circular nodes that lists the index into the array where
x was found. If x is not present, the algorithm will terminate at one of the
square nodes. Circular nodes are called internal node & square nodes are
called external nodes.
Complexity:
If
n is in the range [2k-1,2k), that means 2k-1 ≤n <2 sup="sup">k
,
then binary search makes at most k element comparisons for a successful search
and either k-1 or k comparisons for an unsuccessful search. In other words the
time for successful search is O(log n) and for Unsuccessful search is Θ(log n).
Successful
Search:
Best
Case
|
Θ(1)
|
Average
|
Θ(log n)
|
Worst
|
Θ(log n)
|
Successful
Search:
Best
Case
|
Θ(log n)
|
Average
|
Θ(log n)
|
Worst
|
Θ(log n)
|
ADVANTAGES
1. In this method elements are eliminated by half each time .So it is very faster than the sequential search.
2. It requires less number of comparisons than sequential search to locate the search key element.
DISADVANTAGES
1. An insertion and deletion of a record requires many records in the existing table be physically moved in order to maintain the records in sequential order.
2. The ratio between insertion/deletion and search time is very high.
Implementation:
1. Recursive Algorithm using C:
#include
#include
int BinSearch(int[],int,int,int);
void Sort(int[],int);
int main()
{
int a[25],i=0,x,n,ch;
printf("Enter
Number of Elements:");
scanf("%d",&n);
printf("Enter
Elements:\n");
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
Sort(a,n);
printf("Given
Elements:\n");
for(i=1;i<=n;i++)
printf("%d
",a[i]);
do
{
printf("\nEnter
Element to be Search:");
scanf("%d",&x);
if(BinSearch(a,1,n,x))
printf("\nElement Found\n");
else
printf("\nElement Not Found\n");
printf("Do you want
to search again(0-NO/1-YES)? ");
scanf("%d",&ch);
if(ch==0) exit(0);
}while(ch==1);
return 0;
}
void Sort(int a[],int size)
{
int i,j;
for(i=1;i<=size;i++)
{
for(j=i+1;j<=size;j++)
{
if(a[i]>a[j])
{
int t=a[i];
a[i]=a[j];
a[j]=t;
}
}
}
}
int BinSearch(int a[],int i,int l,int x)
{
int mid,flag=0;
if(i==l)
{
if(x==a[i]) return
i;
else return 0;
}
else
{
mid=(i+l)/2;
if(x==a[mid]) return
mid;
else return
BinSearch(a,mid+1,l,x);
}
}
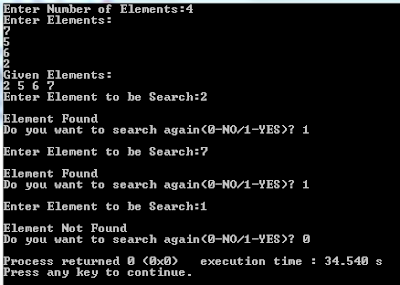
Output:
2. Recursive Algorithm using C++:
#include
#include
using namespace std;
class BinarySearch
{
public:
int
BinSearch(int a[], int i,int l,int x);
void
Sort(int a[],int size);
};
void BinarySearch :: Sort(int a[],int size)
{
for(int i=1;i<=size;i++)
{
for(int j=i+1;j<=size;j++)
{
if(a[i]>a[j])
{
int t=a[i];
a[i]=a[j];
a[j]=t;
}
}
}
}
int BinarySearch :: BinSearch(int a[],int
i,int l,int x)
{
int
mid,flag=0;
if(i==l)
{
if(x==a[i]) return i;
else return 0;
}
else
{
mid=(i+l)/2;
if(x==a[mid]) return mid;
else return BinSearch(a,mid+1,l,x);
}
}
int main()
{
BinarySearch obj;
int
a[25],i=0,x,n,ch;
cout<<"Enter Number of Elements:";
cin>>n;
cout<<"Enter Elements:"<
for(i=1;i<=n;i++)
cin>>a[i];
do
{
obj.Sort(a,n);
cout<<"Given Array:"<
for(i=1;i<=n;i++)
cout<<"Enter Element to be Search:";
cin>>x;
if(obj.BinSearch(a,1,n,x))
cout<<"\nElement Found";
else
cout<<"\nElement Not Found";
cout<
cout<<"Do you want to search again(0-NO/1-YES)? ";
cin>>ch;
}while(ch==1);
return 0;
}
Output:
3. Recursive Algorithm using JAVA:
import java.util.Scanner;
public class BinarySearch
{
public
static void main(String args[])
{
Scanner
s=new Scanner(System.in);
System.out.print("Enter Number of Elements:");
int n=s.nextInt();
int i;
int[] a=new int[n];
System.out.println("Enter Elements:");
a[i]=s.nextInt();
Sort(a);
System.out.println("Given Elements:");
System.out.print(a[i]+" ");
System.out.println();
int ch;
do
{
System.out.print("Enter Element to be Search:");
int t=s.nextInt();
if(Search(a,0,a.length-1,t))
System.out.println("Element Found");
else
System.out.println("Element Not Found");
System.out.println("Do you want to Search again(0-NO/1-YES)?
");
ch=s.nextInt();
if(ch==0)
System.exit(0);
}while(ch==1);
}
public static void Sort(int[] a)
{
{
{
if(a[i]>a[j])
{
int t=a[i];
a[i]=a[j];
a[j]=t;
}
}
}
}
public
static boolean Search(int[] a,int low,int high,int t)
{
int
l,h,mid;
l=low;
h=high;
return false;
mid=(l+h)/2;
if(a[mid]==t)
return true;
else
{
if(a[mid]
return
Search(a,mid+1,h,t);
else
return
Search(a,0,mid-1,t);
}
}
}
Output:


No comments:
Post a Comment